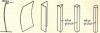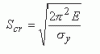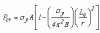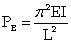Leaderboard

here is a sample of geo-technical report to make you awake All_Image Referencing_Zoning Bylaw Amendment Application_Image Reference_Geotechnical Study - Slope Stability Study D02-02-11-0023.PDF

Here, My fav on diaphargms Diaphragm behavior and idealizations Rigid diaphragms, symmetry, and relative stiffness All frames equal stiffness Symmetrically arranged & equal stiffness means equal resistance Under the rigid diaphragm idealization, the symmetrically arranged identical frames experience the same deflection, and provide equal resistance. Center frame is twice as stiff All frames equal stiffness Third frame is twice as stiff All frames equal stiffness Third frame is twice as stiff Third frame is twice as stiff Concrete slab Ideal rigid diaphragm Concrete slab

Here is a quick tutorial about how to create a new post in forums. For the purpose of tutorial, lets say you want to start a new topic in "Seismic Design". See the attached images as they explain detail about posting. Step 1: Click "Seismic Design" Forum from main index. Step 2: Click on "Start New Topic" Button on top right corner. Step 3: Fill out the required fields as explained in the attached image. That is it! Should you have any questions about posting, please ask below. Many Thanks!

A column is essentially a vertical member designed to transmit a compressive load. Being a compression member, it is reasonable to suppose that a column would fail by crushing of the material when the load reached a high enough value, but for most columns failure occurs at a lower load than the crushing strength; this is because most columns are relatively slender, i.e. they are long in relation to their lateral dimensions which are termed as stocky columns. It is generally seen that when a slender member is loaded in compression, as for example when a slender garden cane is leaned on rather heavily, it will bow sideways or buckle, and if the load is then increased further the cane will eventually fail in bending. If, on the other hand, a stocky column is used, one with a low length to breadth ratio, then a crushing mode of failure is more likely than a buckling mode. For example, if a block of timber 50 mm x 50 mm x 100 mm high were loaded in compression, one could not imagine it failing by buckling. Thus the normal compression elements, length and lateral dimension play a part in determining the mode of failure that will result. Also, for a given section, there will be a critical length of the compression member below which it will be crushed and above which it will buckle. The shape of a column is also very important. For example, a sheet of cardboard has practically no strength as a column, but if bent to form an angle section or other shapes as shown below, it is capable of supporting a load It follows that by intelligent use of available material, economical columns can be constructed. Buckling of slender columns and struts If a long thin flexible rod is loaded longitudinally in compression, it is noticeable that it deflects readily near the mid point of its length with a considerable amount of displacement. The phenomenon is called BUCKLING and occurs when the stresses in the rod are still well below those required to cause a shearing type failure. However, if the length of the rod is gradually reduced, whilst still applying the axial load, a length is eventually reached below which the rod will not buckle. Its failure will be internal. I.e. material failure rather than structural distortion. Columns and struts may therefore be described as either SHORT(stocky) or SLENDER depending on its mode of failure. A short column or strut will fail internally by yielding in the case of ductile materials, such as mild steel, or by shearing in the case of brittle materials such as concrete. A slender column or strut will fail by buckling, where a relatively large bending distortion will develop along its length. The member does not collapse immediately but remains in bent equilibrium unless the yield strength of the material has been exceeded. The buckling phenomenon is an example of unstable equilibrium, whereas the behaviour of a short strut is that of stable equilibrium. The axial load to cause buckling is called the critical load (P). For a given load, a critical length may also be deduced. In the case of slender structural columns or struts, the critical buckling load and the critical length depend upon a number of factors, such as the shape and size of the cross-section, the relationship between the length of the column and its lateral dimensions and the degree of fixity at both ends. For a strut of given length which is pinned at both ends, the minimum load at which buckling will occur may be determined using a mathematical analysis which produces what is known as the EULER FORMULA. The Swiss mathematician, Leonhard Euler (1707 – 83), calculated the load at which a column would buckle if it were axially loaded and pinned at its ends. Thus, the Euler buckling load for an axially loaded pin ended column is given by: PE = the Euler buckling load E = Young’s modulus for the material I = the least second moment of area of the section L = the length of the strut between the pinned ends The magnitude of the buckling load given by this formula is the appropriate value for initially straight struts which are pinned at both ends and are subject to an axial load only. In the cases where one end is fixed and the other end is pinned, or where both ends are fixed, the effective length has to be determined by multiplying the length between supports by an effective length factor. 1. Both ends pinned Effective length = actual length x 1.0 2. Both ends fixed Effective length = actual length x 0.5 3. One end pinned other end fixed Effective length = actual length x 0.7 4. One end fixed, other end completely free Effective length = actual length x 2.0 Effective Length Constant Table Column Boundary Effective Length Constant **C Free - Free 1.0 Fixed - Free 2.0 Fixed - Pinned .707 Fixed - Guided 1.0 Fixed - Fixed .5 Guide - Free 2.0 Guided - Pinned 2.0 Guided - Guided 1.0 Pinned - Free 1.0 Pinned - Pinned 1.0 In practice, the assumptions of the Euler formula rarely hold good and some bending occurs in the strut, causing bending stresses. Also the initial straightness and eccentricity of loading are almost impossible to produce in practice with any reasonable degree of accuracy. Therefore several empirical formulae have been developed for practical use. The Rankine-Gordon formula and the Perry-Robertson formula. Perry-Robertson is the one most used but it is rather complex and so tables have been produced to assist the designer and these can be found in the respective codes of practice. The safe axial load depends on: A = area of cross-section r = least radius of gyration of the section Le = effective length (takes into account length and end conditions). The safe stress depends upon: Slenderness ratio = Le/r Where r = (I/A)1/2 I= moment of inertia A= cross sectional area If the slenderness ratio > (greater than) critical slenderness ratio, then the column is treated as a long column and the Euler buckling formula is applicable. If slenderness ratio is < (less than) the critical slenderness ratio, the column is treated as a short column. In short columns, failure may occur by compression without significant buckling and at stresses exceeding the proportional limit. For this condition, Johnson's formula is applicable: For columns that fail subsequent to the onset of inelastic behavior, the constant of proportionality must be used rather than the modulus of elasticity (Engesser formula). The constant of proportionality, Et, is the slope of the stress-strain diagram beyond the proportional limit, termed the tangent modulus. Note within the linearly elastic range, E = Et. Because of the problems previously mentioned with the Euler equation, the effective length factors are modified to take into account these practical limitations. 1. Both ends pinned Effective length = actual length x 1.0 2. Both ends fixed Effective length = actual length x 0.7 3. One end pinned, other end fixed Effective length = actual length x 0.85 4. One end fixed, other end completely free Effective length = actual length x 2.0 Note: These values for effective length factor apply to design to the current BS but may well vary in the new Euro Codes and thus reference should be made to the appropriate Euro Code for actual design values.

where you heard/read this term? In Pakistan we use US codes and they use the term short column.Strength of Short/stocky columns is governed by the material strength of cross- section and is not effected by the length of column. Though local buckling might occur in steel columns. Then there are slender columns whose strength depends on ratio of length to radius of gyration of section.These columns buckle under compressive loads before material strength of their cross-section can reach.

thanx!!!

Code does require us to use a minimum of six bars for spirals, it does not mention circular cross section in that specification. Code requires minimum of 4 bars for circular/rectangular ties. But we can still use 4 bars in circular column as code also states, at many places, that if engineer is able to prove the safety of his design proposal in light of rules of mechanics,material behavior and serviceability requirements, than he can use it. I answered your question keeping in mind that particular member is kind of dummy member, the one which is not an integral part of structural member.

it is very nice step to have separate thread for job posting it is great helping hand for the one in need!!!thanx admin

Diaphragms connect all individual members into a seismic force resisting system. If you have concrete floors, it is imperative that your floor will do the above mentioned job plus distribute the seismic load to all the connecting members too. Diaphragms can be rigid or flexible depending upon their stiffness. For practise in Pakistan, if your flooring is type conc slab > 5" consider your diaphragm to be rigid. A rigid diaphragm distributes forces to connecting members based on connecting members stiffness, where as a flexible diaphragm distributes loading based on tributary areas of supporting members to diaphragm. Take diaphragm as a frame that connects all members, and makes them act together.