Search the Community
Showing results for tags 'risa torsion design'.
Found 1 result
-
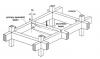
*SEFP Consistent Design* *Torsion: Reinforced Concrete Members * *Doc No: 10-00-CD-0001* *Date: May 24, 2013* Torsional forces, generally speaking, occur in combination with flexural and transverse shear forces. From a design perspective, we need to understand difference between two torsion t...
- 15 replies
-
- 11
-
-
- torsional stiffness of beams
- risa torsion design
- (and 8 more)
